11 Animation

概述

动画可以视作是模型的扩展：将场景模型表示为关于时间的函数

输出：一系列图像，按顺序观看时产生动态的感觉

• 电影：24fps
• 视频（一般）：30 fps
• 虚拟现实：90 fps

历史

​

​

动画最早用作科学用途，随着技术的进步，加速了动画的发展

​

关键帧动画

给定一些关键的帧，其他中间的过渡部分则通过插值的方式生成出来

​

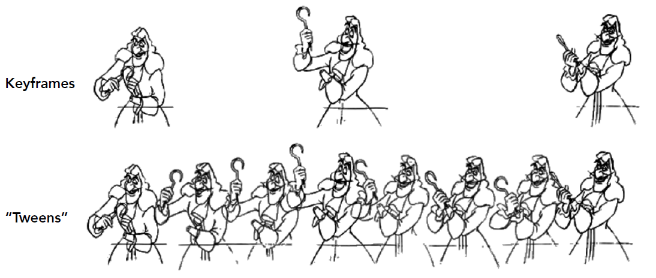
关键帧动画本质是一种插值的技术

• 线性插值的效果通常不太好
• 会使用更平滑的方式进行插值

物理模拟

通过牛顿定律计算物体的后续位置与速度

​

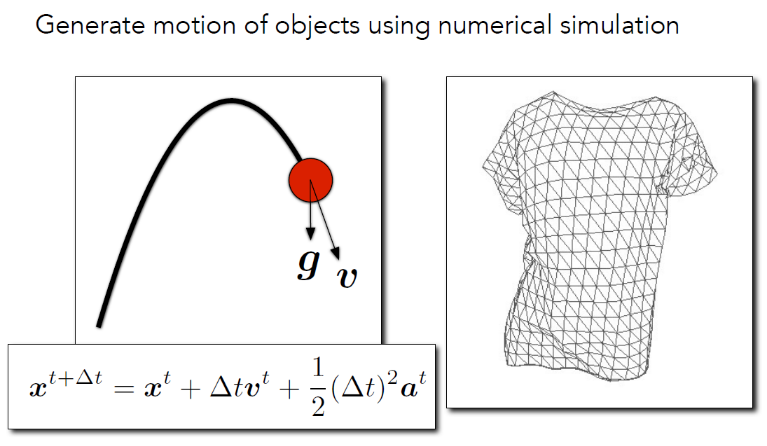
只要正确建立了物体之间的相互作用力，自然可以模拟正确的效果

质点弹簧系统

质点弹簧系统用于模拟物体形变和运动的物理模型。

它将物体离散为若干个质点，质点之间通过弹簧连接，通过计算质点之间的相互作用力来模拟物体的物理行为。

• 质点 ：具有质量但忽略大小和形状的物体，是系统的基本组成单元。每个质点的位置、速度和加速度等状态变量都需要被跟踪和计算。
• 弹簧 ：连接两个质点的弹性元件，其力的计算通常遵循胡克定律，即弹簧力与弹簧的形变量成正比，方向与形变方向相反。公式为 F\=-k*(Δl)，其中 F 为弹簧力，k 为弹簧的劲度系数，Δl 为弹簧的伸长量或压缩量。
• 运动方程 ：根据牛顿第二定律，质点的加速度与所受合力成正比，与质点质量成反比。通过对质点所受的弹簧力以及其他外力（如重力、阻尼力等）进行求和，得到质点的加速度，进而积分得到质点的速度和位置。

在计算机图形学中，可用于模拟布料、毛发、皮肤等柔性体的运动和形变；在物理模拟中，可用于研究物体的振动、碰撞等物理现象。

对于复杂的面，质点之间会进行额外的连接，以便更好的符合实际情况

​

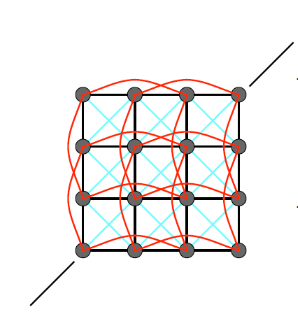
有限元方法

除了质点弹簧系统之外，还有其他的模拟方法，例如有限元方法

有限元方法是一种用于求解物理问题和工程问题的数值计算方法。它将连续的物理域离散为有限个单元，通过在单元上建立近似方程，并利用变分原理或加权残值法等方法，将原问题转化为代数方程组进行求解。

粒子系统

粒子系统用于模拟由大量微小粒子组成的复杂现象和效果。

每个粒子具有自己的属性，如位置、速度、颜色、大小等，通过对粒子的更新和绘制，可以生成各种逼真的动态效果。

挑战：

• 可能需要大量例子
• 可能需要加速结构（例如，寻找相互作用的最近粒子）

更新： 粒子会在每一帧更新

• 如有需要，创建粒子
• 计算每个粒子的作用力
• 更新每个粒子的位置和速度
• 如有需要，移除死亡粒子
• 渲染粒子

粒子系统的力：

• 吸引力和排斥力：

  • 引力、电磁力
  • 弹力，推力
• 阻尼力：摩擦力，空气阻力

• 碰撞：

  • 墙壁，容器，固定物件
  • 动态物体，角色身体部位

运动学

正向运动学

正向运动学是从关节空间到操作空间的映射过程。

它主要研究机械臂（或类似的运动学结构）的各个关节角度（或位置）与末端执行器在空间中的位置和姿态之间的关系。

简单来说，当已知机械臂各个关节的参数（如旋转角度或伸缩长度）时，通过正向运动学可以计算出末端执行器在空间中的具体位置和姿态。

逆向运动学

逆向运动学是正向运动学的逆过程。

它的目标是确定机械臂的关节角度（或位置），使得末端执行器能够准确地到达指定的空间位置和姿态。

也就是说，已知末端执行器期望的位置和姿态，要求解出各个关节的参数，以实现该位置和姿态。

值得注意的是，对于给定的末端位置，可能存在多个解或不一定存在解满足条件

Rigging

Rigging是指为 3D 模型创建骨骼结构和控制系统，以便能够对模型进行动画制作的过程。

• 骨骼绑定 ：将骨骼放置在模型内部，例如在人物模型中，将脊柱、四肢等骨骼放在相应的位置，以模拟人体骨骼的分布。
• 蒙皮 ：也称为权重分配。这是将模型的几何体与骨骼关联起来的过程。通过蒙皮，定义了模型的每个部分受哪些骨骼的控制以及控制的程度。例如，在手臂模型上，赋予手臂骨骼对皮肤的控制权重，使得当骨骼移动时，模型的皮肤也随之变形。
• 动画控制 ：创建各种控制器，如控制面板、滑块、旋钮等，方便动画师控制角色的动作。例如，一个旋转控制器可以用来控制手臂的弯曲角度。

Rigging 是正向运动学和逆向运动学在角色动画中的具体应用。在 Rigging 过程中，会利用正向运动学来计算骨骼的运动关系，例如，当动画师调整手臂骨骼的旋转角度时，模型的手臂会按照正向运动学的原理进行相应的位置变化。

同时，也会使用逆向运动学来解决一些复杂的运动问题。比如，在角色行走时，脚部的位置和姿态是已知的，通过逆向运动学可以计算出腿部骨骼的运动角度，以实现自然的行走动作。

动作捕捉

Motion Capture

通过在物体（通常是演员的身体或物体表面）上放置标记点（Marker）或传感器，利用光学、惯性、电磁等技术捕捉这些标记点或传感器的位置和运动数据，然后将这些数据转换为数字信号，用于驱动虚拟角色或物体的运动。

Facial Motion Capture

主要针对演员的面部表情和口型进行捕捉，通过特定的技术获取面部肌肉的运动、五官的变化等数据，将其转化为数字信号，用于驱动虚拟角色的面部表情和口型。

单粒子模拟

已知某个物体在某个时刻的速度和位置，求解一段时间之后它的位置和速度。

很多情况下物体不是匀速运动，粒子在不同的位置具有的速度不一致。

假设存在一个速度场，对于一个粒子来说，只要知道它的位置，就能够知道它的速度。

欧拉方法

取一个很小的时间${\Delta}t$，可以认为，在这个时间里，物体是做匀加速直线运动

那么，可以通过逐步递进的方式，求解最终的物体位置

$x^{t + {\Delta}t} = x^t + v^t {\Delta}t \\ v^{t + {\Delta}t} = v^t + a^t {\Delta}t $

通过上面的公式反复迭代，可以最终得到结果

缺陷：

• 因为每一次的模拟都是近似，随着迭代次数的增加，误差会逐渐增大
• 稳定性差，难以适用于曲线：在曲线上的误差会更大，更容易偏离曲线轨迹

中点法

中点法是一种改进方法，思路是算两次欧拉方法

​

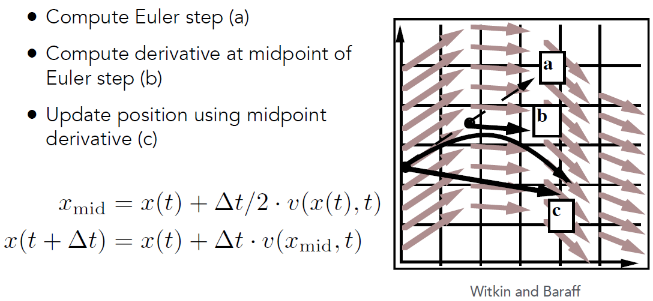
对于一次单独的迭代来说

• 先算一次，得到路径a
• 取路径的中点b的速度
• 应用中点的速度重新算一次，得到路径c

自适应补偿

​

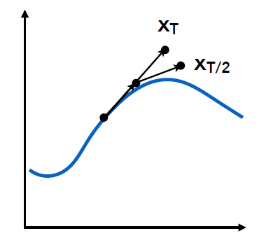
自适应补偿的思路是：

• 将步长减半，比较步长减半与不减半的差异
• 如果差异过大，则继续步长减半的做法，最终得到合适的自适应步长

隐式欧拉方法

原来的欧拉方法，是用上个时刻的速度，加速度来更新位置

而隐式欧拉方法，是用这个时刻的速度和加速度来更新从上一时刻到这一时刻的位置

$x^{t + {\Delta}t} = x^t + v^{t+{\Delta}t} {\Delta}t \\ v^{t + {\Delta}t} = v^t + a^{t+{\Delta}t} {\Delta}t $

这种情况需要提前求解速度和加速度

量化误差

如何确定 / 量化 “稳定性”？

• 我们使用局部截断误差（每一步） / 总累积误差（整体）
• 绝对值无关紧要，但相对于步长的阶（order）很重要

• 隐式欧拉方法具有一阶精度，这意味着：

  • 局部截断误差：$O(h^2)$
  • 全局截断误差：$O(h)$（h 是步长，即 Δt）

• 对 O(h) 的理解：

  • 如果我们将 h 减半，我们可以期望误差也会减半。

阶数越高越好

Runge-Kutta Families —— RK4

这是一类用于求解常微分方程（ODEs）的先进方法。

• 特别擅长处理非线性问题。
• 其四阶版本最为广泛使用，通常被称为 RK4。

Position-Based / Verlet Intergration

思想：

• 在修改后的欧拉前向步之后，约束粒子的位置，以防止发散和不稳定的行为。
• 使用约束后的位置来计算速度。
• 这两种方法都会耗散能量，从而增加稳定性。

优缺点：

• 快速且简单。
• 不基于物理原理，会耗散能量（存在误差）。

刚体模拟

刚体不会发生形变，其运动等效于质点，

除了速度和位置之外，还存在角度和角速度

流体模拟

Position-Based

关键思想

• 假设水由小的刚体球组成
• 假设水不可被压缩（即密度恒定）
• 因此，只要某处密度发生变化，就应该通过改变粒子位置来进行“修正”，这象征着水的流动

任何一个点处的密度，都是任何一个其他的小球的位置的函数

使用梯度下降法来实现粒子位置更新

欧拉方法与拉格朗日方法

拉格朗日方法（质点法）：假设物体是由多个小粒子组成

​

欧拉方法（网格法）：将空间分割为网格，考虑网格随时间的变化情况

物质点法

Material Point Method, MPM

一种混合方法，结合了欧拉（Eulerian）和拉格朗日（Lagrangian）观点：

• 拉格朗日观点：考虑携带材料属性的粒子。
• 欧拉观点：使用网格进行数值积分。
• 交互过程：粒子将属性传递给网格，网格执行更新，然后通过插值将结果反馈回粒子。

‍