07 Materials and Appearances

有不同的材质，在某些光照下，就会表示出不同的外观，所以说外观是光线和材质共同作用的结果。

因此，在研究材质的时候，实际上研究的是光线如何与材质进行作用

图形学中的材质

材质可以通过非物理的方式用贴图，法线来模拟

从渲染方程来看，可以说 Material == BRDF，即决定了光如何进行反射与折射

漫反射材质

漫反射材质无光泽，无反射，例如陶瓷，木头

​

在Blinn-Phong模型中，漫反射系数是一个经验系数，其取值范围为(0, 1)

$L_d = K_d \left( \frac{I}{r^2} \right) \max(0, \mathbf{n} \cdot \mathbf{l})$

在渲染方程中，类似地，可以推出对应的漫反射系数

假设入射光是均匀的，即各个方向都是均匀的，那么入射光的能量等于出射光的能量

假设$f_{r}$和$L_{i}$都是常数，则有

$\begin{aligned} L_{o}\left(\omega_{o}\right) &=\int_{H^{2}} f_{r} L_{i}\left(\omega_{i}\right) \cos \theta_{i} \mathrm{d} \omega_{i} \\ &=f_{r} L_{i} \int_{H^{2}} \cos \theta_{i} \mathrm{d} \omega_{i} \\ &=\pi f_{r} L_{i} \end{aligned}$

因此，有

$f_{r}=\frac{\rho}{\pi}$

可以认为ρ就是反射率，其取值范围是0~1

光泽材质

有光泽，无反射的材质，例如金属

​

镜面材质

镜面材质用于透明，半透明的物体，例如水，玻璃

​

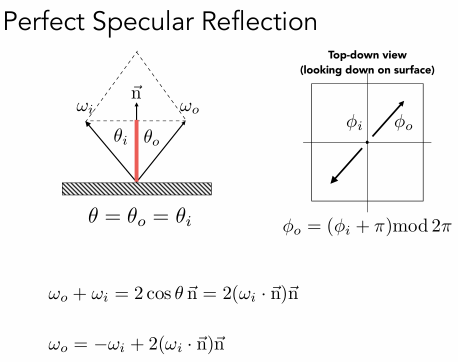
完美镜面反射

完美镜面反射的反射角是可算的，左图是正视图，右图是俯视图

​​​

镜面折射

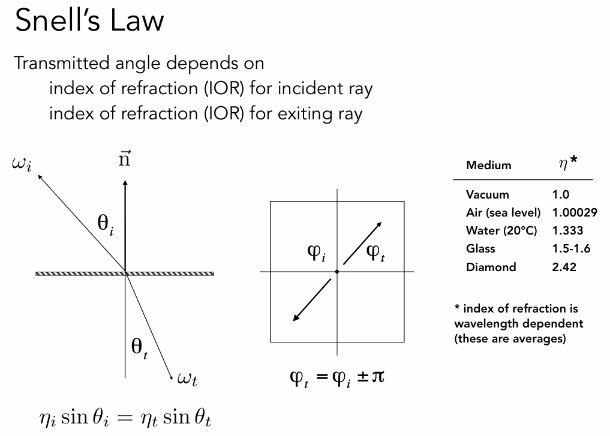
光从一种介质入射到另一种介质时，可能会发生折射现象

折射定律：

（1）折射光线位于入射光线和界面法线所决定的平面内；

（2）折射线和入射线分别在法线的两侧；

（3）入射角i的正弦和折射角i′的正弦的比值，对折射率一定的两种媒质来说是一个常数。

​

​

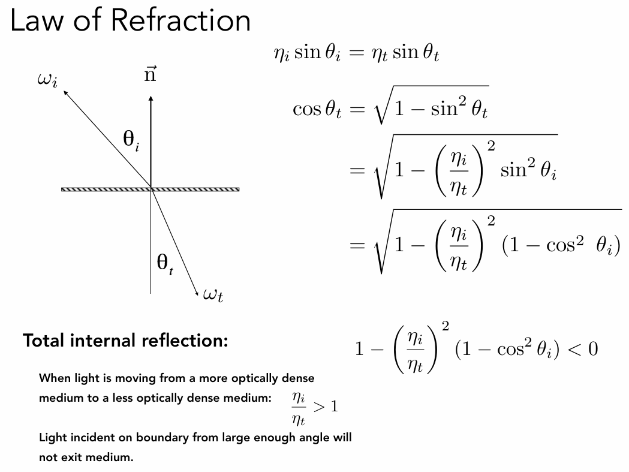
可以看出，某些情况$cos\theta_{i}$不存在，不会存在折射现象，此时会发生全反射

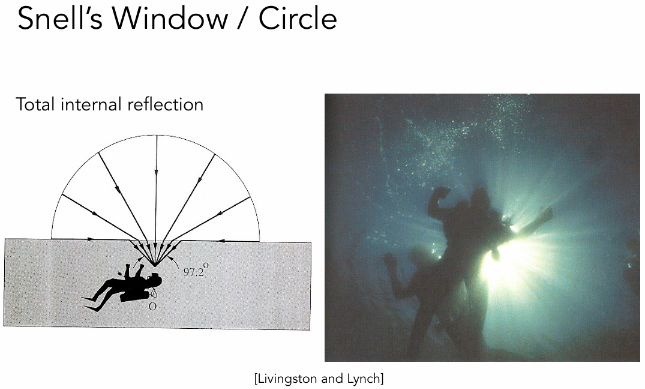
斯涅耳窗： 从水底看，由于折射现象的存在，人只能看到锥形视野范围内的光

​

BTDF

双向反射分布函数（BRDF）

双向折射(透射)分布函数（BTDF）

BRDF和BTDF统称为双向散射分布函数（BSDF）

菲涅耳反射

根据光的反射规律可知，折射反射的程度取决于观察者的角度。简单的讲，就是视线垂直于表面时，反射较弱，而当视线非垂直表面时，夹角越小，反射越明显

例如站在湖边，低头看脚下的水，会发现水是透明的，但是看远处的湖面，湖面更像一面镜子

此外，入射角相同，不同材质的菲涅尔项也不一样

​

上面的s和p跟光的波动有关，这里只需要知道有这么个东西可以算就行了

微表面理论

微表面理论认为，所谓的平面实际上是由不同方面的微观表面组成

​

对于粗糙和光滑的平面来说，实际上就是微观表面的朝向聚集不同

​

BRDF

根据微表面模型，BRDF方程可以进一步优化，表示为

​​​

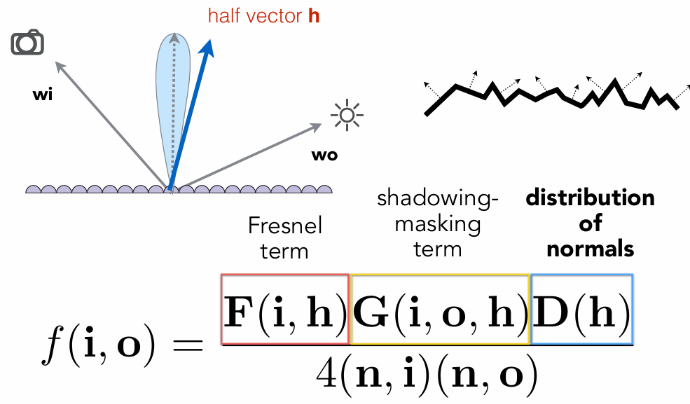
• F为菲涅尔项
• D为微平面的法线分布，用于查询半程向量h
• G为几何项：由于在微表面上，对于那些几乎和表面平行的入射光，很容易发生互相遮挡的现象，从而使得部分微表面失去作用，我们把这种光线角度称为掠射角度（Grazing Angle），在这种角度下的着色会非常亮，G项就起到了一定的修正作用

微表面模型可以得到非常非常真实的渲染结果，是基于物理的方法，也是现在的state of art

各向同性/各向异性

材质可以分为两类

• 各向同性：各项同性材料的微表面的方向是均匀的
• 各向异性：各项异性材料的微表面的方向是不均匀的

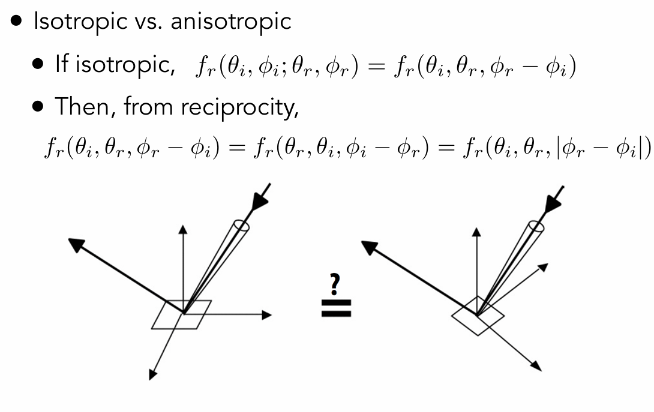
如果入射光和出射光做一定方位角的旋转前后，BRDF方程不变，那么这 种材质就是各向同性的，反之则为各向异性

BRDF总结

性质

非负性： 描述能量分布

线性性： 可以被拆分成不同项的线性组合（ambient，diffuse，specular）

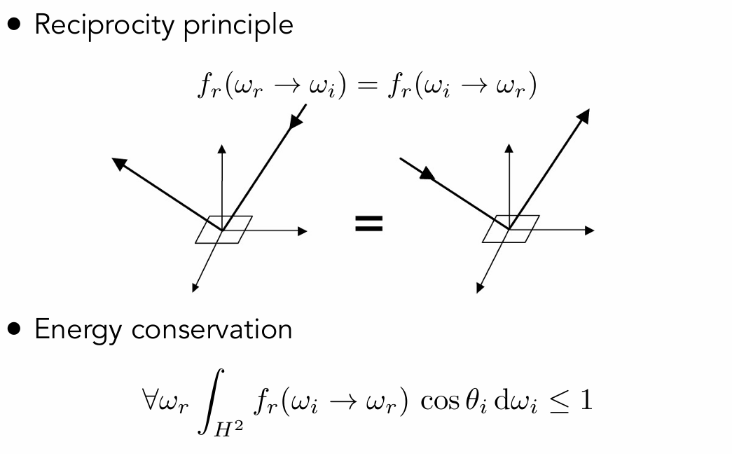
可逆性： 调换入射出射方向，BRDF渲染结果严格不变

能量守恒： 出射光线的能量永远不能超过入射光线的能量

各向同/异性： 如果是各项同性材质，则BRDF值只和相对方位角有关，四维的BRDF材质可以被降维为三维，并且根据可逆性，结果不需要考虑方位角的正负

​

​

​

BRDF的测量

BRDF虽然在理论上可计算，但并不完全符合实际

因此，实验上的测量可以无需理论推导而直接使用

​

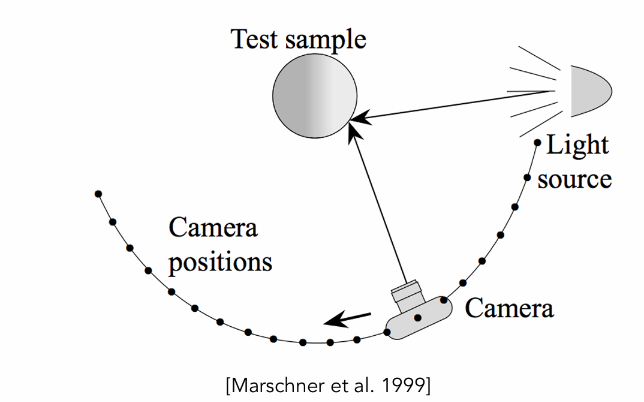
给定一个着色点，通过改变入射和出射的角度（改变光源与相机位置）进行测量

foreach outgoing direction wo
	move light to illuminate surface with a thin beam from wo
 	for each incoming direction wi
		move sensor to be at direction wi from surface
 		measure incident radiance

如算法伪代码所示，这样测出来的BRDF是四维的，这样的测量是非常费时的

为了提高效率，我们可以尽量让材质呈各向同性

就像之前说的，这不仅可以让BRDF从四维降至三维，还能由光路可逆性再砍去一半的测量

‍