05 Geometry
05 Geometry
三维几何表示
隐式几何
用空间中的满足一定条件的点的集合来表示面,隐式几何不会表示点的具体位置信息,而是告诉我们这些点满足的函数关系
我们很难看出隐式想表达的形状是什么,但对于判断点的位置关系(在内,在外还是在表面)会很方便
显式几何
直接给出点的位置,或者可以进行参数映射;然而想要判断内外时,显式的表达就很难进行表示
点云
用空间中一堆点的集合来表示物体,只要点足够密集,就看不到点与点之间的空隙,理论上可以表示任何几何,通常三维扫描得到的结果就是点云(点云可以转变为三角形)
多边形网格
或许是目前最为广为流传的三维几何表达方式
曲线与曲线
贝塞尔曲线
用一系列给定的控制点来定义一个曲线
n阶贝塞尔曲线有n+1个控制点
2阶贝塞尔曲线如下:
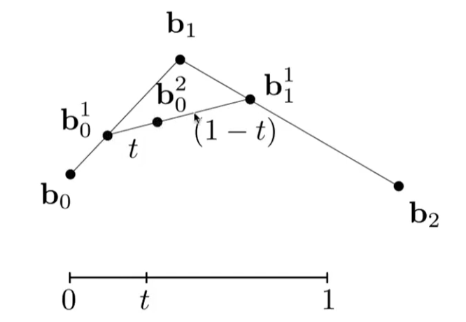
3阶贝塞尔曲线如下:
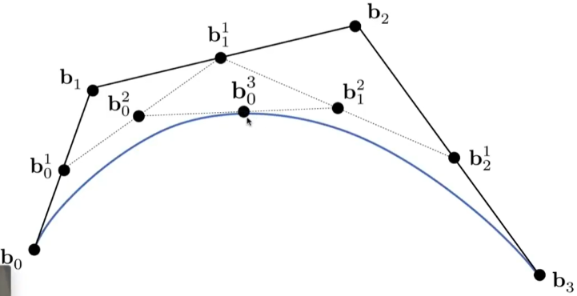
性质:
- 过起点终点,起始切线方向为前两个点连接的方向,终止切线方向为结尾两个点连接的方向
- 在仿射变换下,只需要对顶点做仿射变换,就能得到这个贝塞尔曲线在仿射变换下的结果
凸包性质: 贝塞尔曲线始终会在包含了所有控制点的最小凸多边形中,而不是按照控制点的顺序围成的最小多边形
逐段贝塞尔曲线将一个完整的曲线划分为多段贝塞尔曲线,一般每段贝塞尔曲线用四个点来控制
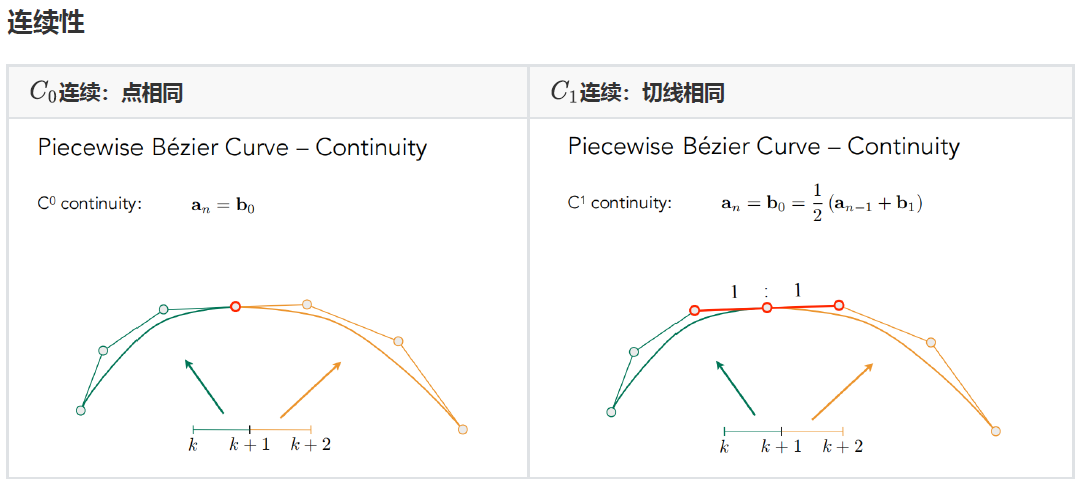
B样条曲线
贝塞尔曲线适合表示简单的曲线,但对于更复杂的曲线来说,由于贝塞尔曲线连续性较差,拼接多段贝塞尔曲线时,需要特别设置控制点以保证连续性。
B样条曲线的优势:
- B样条曲线的局部性使得修改曲线的局部形状更加方便。
- B样条曲线可以很容易地实现高阶连续性,这对于创建平滑的曲线和曲面非常重要。
- B样条曲线可以通过调整控制点和节点向量实现更复杂的曲线形状。
具体有点复杂,没讲
贝塞尔曲面
u方向上画出四条贝塞尔曲线后,在这四个线上再取四个点,并认为这是个点是一组新的贝塞尔曲线的控制点,这些点在空间内向v方向扫描,便形成了贝塞尔曲面
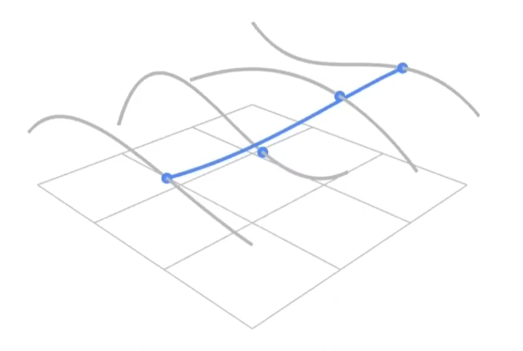
如上图,蓝色的线滑动,就形成了相应曲面
更复杂的问题,比如不同贝塞尔曲面之间的无缝衔接,没有讲
曲面细分与简化
曲面细分(网格细分)
Mesh Subdivision
将一个网格,细分为多个网格,增加面数,使得模型更加光滑
Loop细分(算法创始人的名字叫Loop)
- 连接各边中点,并重新改变各个顶点位置,从而创造出更多三角形面,使得表面更加光滑
Catmull-Clark 细分
- loop细分只适用于三角形网格,而对于非三角形网格的细分,就需要借助catmull-clark算法
- catmull-clark算法定义,面分为两种——四边形面和非四边面,点也分两种——度为4的奇异点和其余的非奇异点(度为4意思是该点相连的边数为4)
具体做法:
- 对每个非四边面都取其中的一个点(重心或者其他点),将其与该面的边的中点相连,
- 在这个过程中,会引入一个新的奇异点,但是在第一次细分以后,所有的非四边面都变为了四边形面
- 接着我们进行后续的细分,直到曲面细分到符合我们的要求,后续的细分将不会引入新的奇异点
网格简化
Mesh Simplication
边坍缩
可以这样想象,边坍缩就是将一条边的两个端点靠近到一起,在这个过程中,这条边邻接的面会坍缩成边
二次误差度量:坍缩后的点和原本几个边(面)的距离的平方和最小
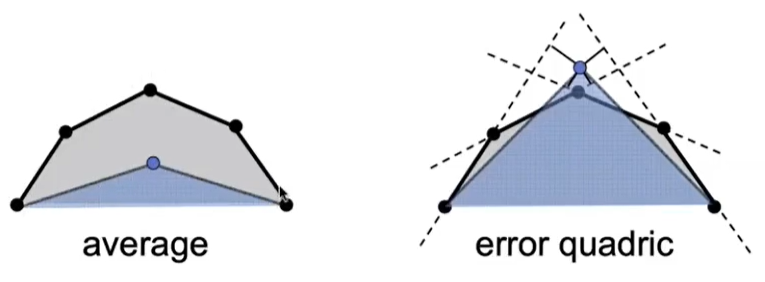
如上图,五个顶点简化为三个顶点,用蓝色的点来代替三个顶点,使得替代后的三角形和原来的五边形近似。
我们就可以采用二次度量误差的方法,计算蓝色顶点的最优位置,使得蓝色顶点到原来各条边距离平方和值最小
二次度量误差要更新
需要注意的是,对一条边做一次坍缩后,其他边也跟着变了,他们对应的二次误差必须被重新计算
所以需要从二次度量误差中选最小的,取完最小的之后,我们要对它们的二次误差做一次更新,我们要用到优先队列 / 堆这种数据结构,这种数据结构能让我们能取得二次误差最小值的同时也能动态更新其他受影响的元素