03 Rasterization

视口变换

上一节中，已经将物体变换到裁剪空间$[-1,1]^3$中，接下来，需要完成到屏幕空间的映射

其变换矩阵如下：

$\mathbf{M_{\text{viewport}}} = \begin{bmatrix} \frac{\text{width}}{2} & 0 & 0 & \frac{\text{width}}{2} \\ 0 & \frac{\text{height}}{2} & 0 & \frac{\text{height}}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

采样

光栅化——采样

• 屏幕是一个二维数组的标准数据集，是离散的，是一个典型的光栅成像设备。
• 经过矩阵变换后，再把屏幕空间中的多边形打散成三角形，成像到屏幕上，这就是光栅化的大致流程
• 最简单的光栅化方法是采样。具体来说，是看三角形和像素的位置关系，这一步要借助于向量乘法判断。

采样优化

• 光栅化时的，为了显示某个三角形。我们需要判断屏幕上的像素和三角形的位置关系。只有在三角形内部的像素点才会被赋予颜色。

轴向包围盒（AABB）

• 借助于轴向包围盒，我们可以在光栅化前先判断像素点是否在三角形所在包围盒内，若不在则直接忽略。

走样（锯齿）

• 由于分辨率的限制，可能出现走样的情况。
• 要解决普通的反走样，我们先对原图进行模糊处理，再进行采样，可以一定程度上解决走样问题。
• 注意反过来是不可行的

深度缓存 -Zbuffering

• 之前并没有考虑过显示的三角形之间的遮挡关系，为了解决这个问题：
• 最简单的想法就是利用画家算法：由远及近画画，近处画面覆盖远处画面。但是，这种算法无法处理复杂的深度判断，例如三个三角形互相重叠，并不适用。
• Zbuffering算法对每个像素多存一个深度，显示的时候，进行比较来更新显示的像素点。实际编程中，z值越小表示越远。

傅里叶变换

傅里叶级数：把一个周期函数通过最简单的一系列正弦函数来表示。

利用傅里叶变换和逆傅里叶变换，我们可以把一个函数转换为另一个函数。

不同的正余弦函数都有不同的频率，傅里叶变换可以把一个函数转换为不同频率的正余弦函数之和。

​

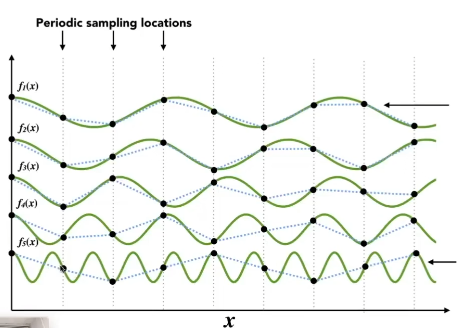
走样的原因：

• 在进行等距采样的时候，越是高频的函数，越容易丢失原始的信息。

• 采样两种截然不同的函数反而可能会得到相同的结果

滤波—傅里叶变换角度

滤波可以认为是去掉某些频率。

对于一张图片，我们可以使用傅里叶变换，把这个图像从时域（其实没有时间信息，只有空间信息，只是叫这个）变换为频域。

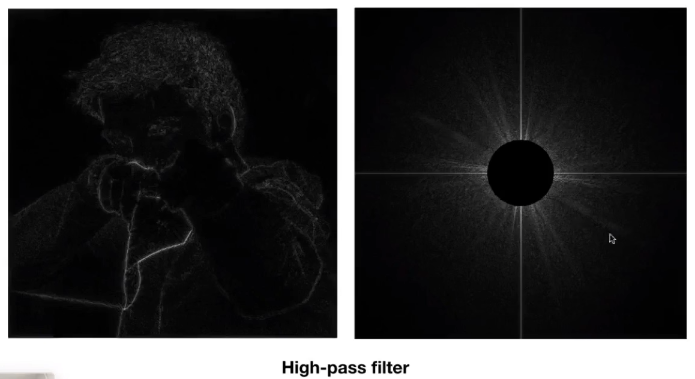
一般的图片进行傅里叶变换之后，得到频谱。中间的是低频信息，四周的是高频信息（下图右）。

​

在图像的边界，也就是颜色变化剧烈的地方，就对应的是高频信息，因此高通滤波之后得到的是一个图片边缘。

​

经过低通滤波之后，图片变得模糊​​

​

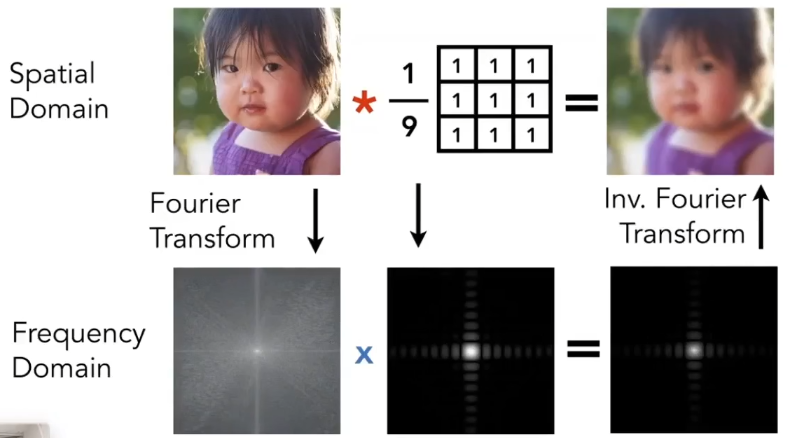
滤波—卷积角度

滤波可以看作是一种卷积。

结论：时域的卷积=频域的乘积。

​

反走样

SSAA

SSAA（Supersampling Anti-Aliasing） ：一个更大的分辨率来渲染场景，然后再把相邻像素值做一个过滤（比如平均等）得到最终的图像。

SSAA可以说是图形学中最简单粗暴的反走样方法，但同时也最有效，唯一的缺点是性能太差。

任何类型的走样归根结底都是因为欠采样，那么我们只需要增加采样数，就可以减轻走样现象。这就是SSAA，所以SSAA简单的来说可以分三步：

（1）在一个像素内取若干个子采样点

（2）对子像素点进行颜色计算（采样）

（3）根据子像素的颜色和位置，利用一个称之为resolve的合成阶段，计算当前像素的最终颜色输出

​

SSAA同时是几何反走样和着色反走样方法，因为它不但增加了当前几何覆盖函数（Coverage）的采样率，也对渲染方程进行了更高频率的采样（单独计算每个子像素的颜色）。

MSAA

由于SSAA在光栅化阶段和片元着色阶段都需要大量的额外计算，开销巨大

MSAA（Multisample Anti-Aliasing） 则只在光栅化阶段，判断一个三角形是否被像素覆盖的时候会计算多个覆盖样本（Coverage sample），但是在pixel shader着色阶段计算像素颜色的时候每个像素还是只计算一次。

例如下图是4xMSAA，三角形只覆盖了4个coverage sample中的2个。所以这个三角形需要生成一个fragment在pixel shader里着色，只不过生成的fragment还是在像素中央（位置，法线等信息插值到像素中央）然后只运行一次pixel shader，最后得到的结果在resolve阶段会乘以0.5，因为这个三角形只cover了一半的sample。

​

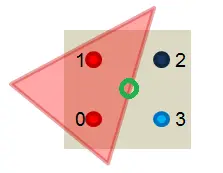
现代所有GPU都在硬件上实现了这个算法，而且在shading的运算量远大于光栅化的今天，这个方法远比SSAA快很多。顺便提一下之前NV的CSAA，它就是更进一步的把coverage sample和depth，stencil test分开了。

由于MSAA拥有硬件支持，相对开销比较小，又能很好地解决几何走样问题，在游戏中应用非常广泛（我们在游戏画质选项中常看到的4x/8x/16x抗锯齿一般说的就是MSAA的子采样点数量分别为4/8/16个）。

MSAA的一个问题就是和延迟渲染并不兼容。延迟渲染的核心是GBuffer（几何缓冲区），它在渲染的第一阶段将颜色、深度、法线等信息存储到多个纹理中。然而，MSAA需要在光栅化阶段对几何信息进行采样，而延迟渲染在光照计算阶段已经丢失了这些几何信息。例如，GBuffer中的深度和法线信息是逐像素存储的，无法直接用于MSAA的子采样处理

因为MSAA这个问题现代引擎里都用的是Post Processing AA这一类技术。这一类东西包括FXAA，TAA等，不依赖于任何硬件，完全用图像处理的方法来搞。

FXAA

FXAA 是由 NVDIA 发明的高效后处理抗锯齿方案，也是目前所有后处理抗锯齿方案里面同等设置下效率最高的抗锯齿算法

原理：找到边界，换成没有锯齿的边界，（图像匹配）非常快

方法和采样无关，采样虽然有误，但是这种方法可以弥补

TAA

原理：利用时序信息，借助前面帧提供的信息

静态场景，相邻两帧同一像素用不同的位置来sample