02 Transformation
02 Transformation
变换
线性变换
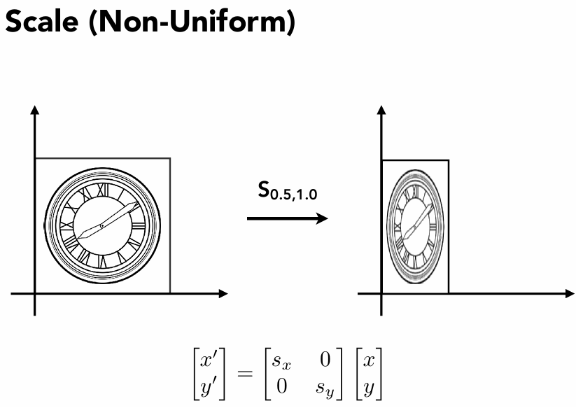
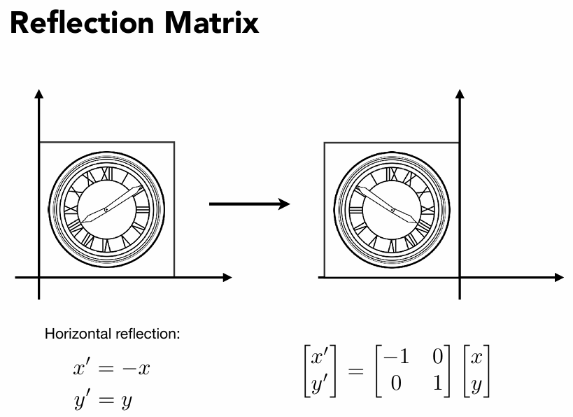
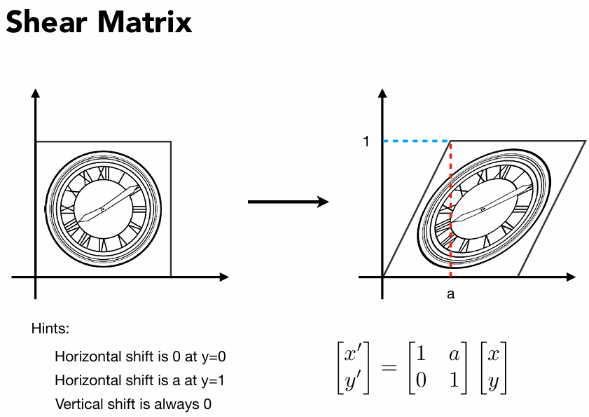
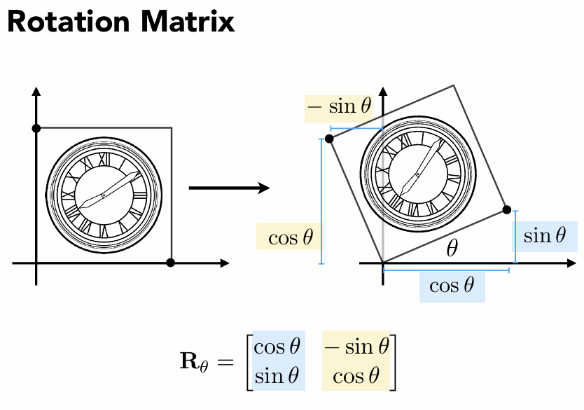
齐次坐标
缩放,对称,切变,旋转,都是线性变换。但是平移变换不是线性变换,不能写成如上形式。
为了统一上面的五种变换方式,我们引入齐次坐标的概念。
用N+1维向量来表示N维坐标,用向量的最后一位数来指明是点还是向量(1表示点,0表示向量)。
对于二维坐标系来说:
- 二维点 $(x, y, 1)^T$
- 二维向量 $(x, y, 0)^T$
矩阵的变换可以表示为:
$\begin{pmatrix} x’ \\ y’ \\ w’ \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + t_x \\ y + t_y \\ 1 \end{pmatrix}$
这样的话,我们可以表示平移。同时通过1或者0也能轻易分辨点还是向量。
在这种情况下,有如下运算:
- 点 + 点 = 点(表示两点的中点)
- 点 + 向量 = 点(表示点沿着某个向量移动)
- 向量 + 向量 = 向量
- 点 - 点 = 两点构成的向量
此外,在齐次坐标中,$\begin{pmatrix} x \\ y \\ w \end{pmatrix} = \begin{pmatrix} x/ \\ y/w \\ 1 \end{pmatrix} $
齐次坐标的二维变换如下:
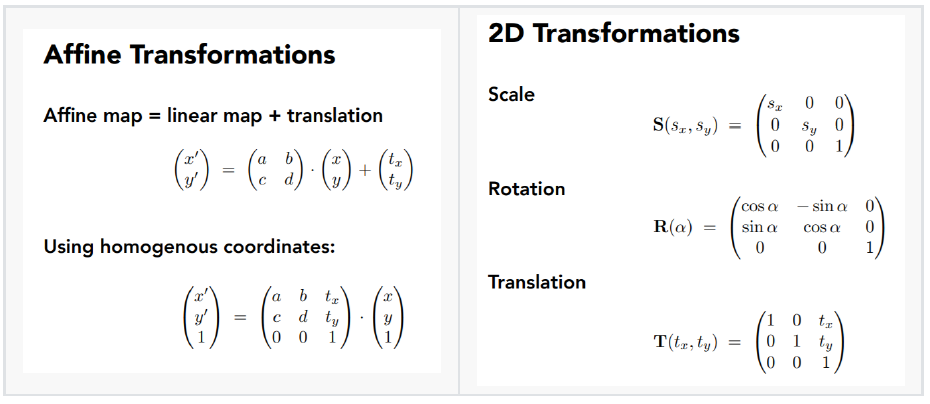
逆变换
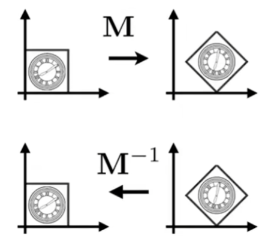
- 通常的旋转操作是绕坐标原点进行的。
- 旋转矩阵的逆 = 旋转矩阵的转置。
复杂变换
复杂的变换可以拆分为多个简单变换的组合。一个符合条件的操作矩阵可以拆分为多个操作矩阵的乘积。
对向量或者点进行复杂变换时,对应的操作矩阵都是左乘运算。
矩阵的乘法不满足交换律:按照同样的数值,先平移再旋转和先旋转再平移,得到的结果很可能不一样。这也符合矩阵的乘法。
矩阵的乘法满足结合律:我们可以先将操作矩阵乘起来,最终合成为一个操作矩阵。
三维变换
平移变换
$T(t_x, t_y, t_z) = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$
缩放变换与反射变换矩阵
$S(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
旋转变换
$R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ R_y(\alpha) = \begin{bmatrix} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ R_z(\alpha) = \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
上面的旋转公式是绕坐标轴旋转,当绕任意轴旋转时:
- 如果这个轴的起点在原点,可使用罗德里格斯公式:罗德里格斯公式Rodrigues'Rotation Formula推导 - 知乎 (zhihu.com)
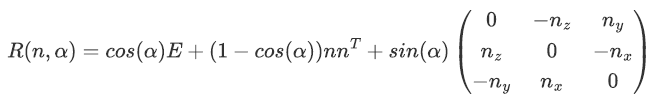
- 如果这个轴的起点不在原点,先整体平移到原点,旋转之后再平移回去
MVP变换
模型变换
Model Transformation
将每个模型的的顶点坐标从局部坐标系变换到世界坐标系
视图/相机变换
View Transformation/Camera Transformation
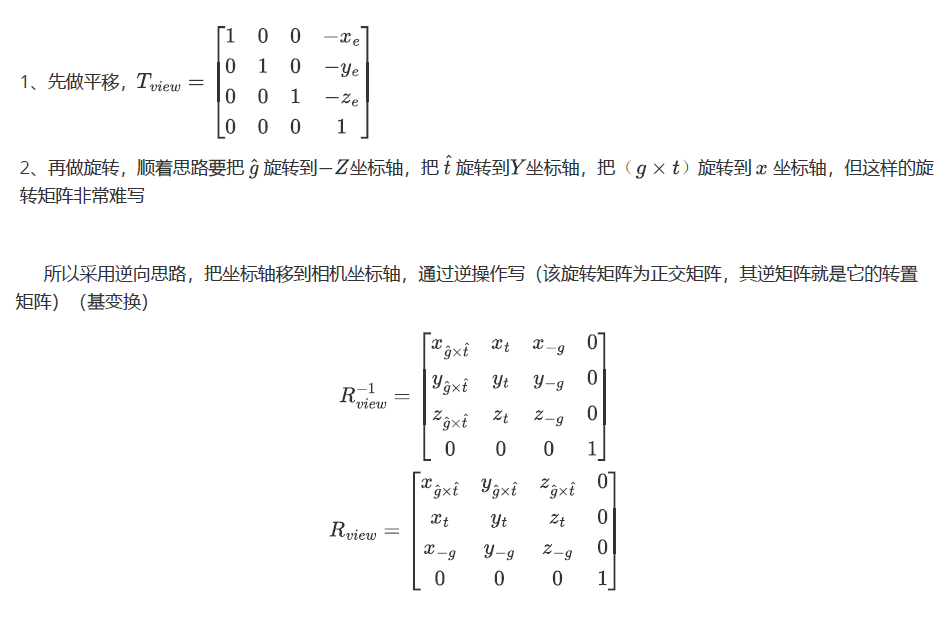
在场景中放置相机。我们规定摄相机的位置始终处于原点,向上的方向是y轴,看向-z轴。这样一来,我们定义好了相机的属性,即位置,垂直方向,视线方向。
视图变换则是将世界坐标系转换到摄像机坐标系
如果摄相机的属性不符合我们的定义,我们可以通过平移变换和旋转变换,将摄像机变换到初始位置。此时,其他所有的物体也应该进行同样的变换以保证相对位置不变。
投影变换
Projection Transformation
有两种投影变换:正交投影(orthographic projection) 与透视投影(perspective projection) 。
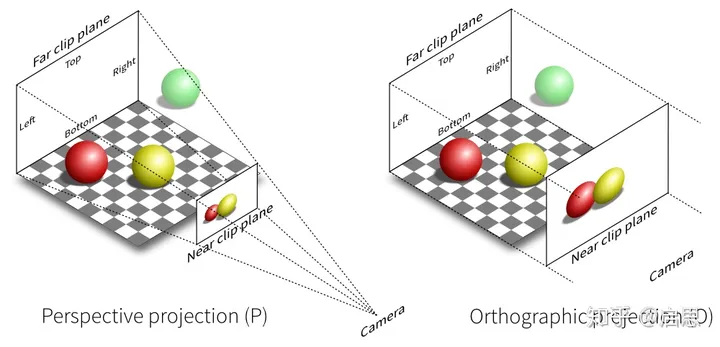
正交投影: 看向物体时将所有物体的z值归0,然后将物体平移并缩放到 [-1,1]^2之间。相机位置无限远,没有远近概念(忽略深度信息)。
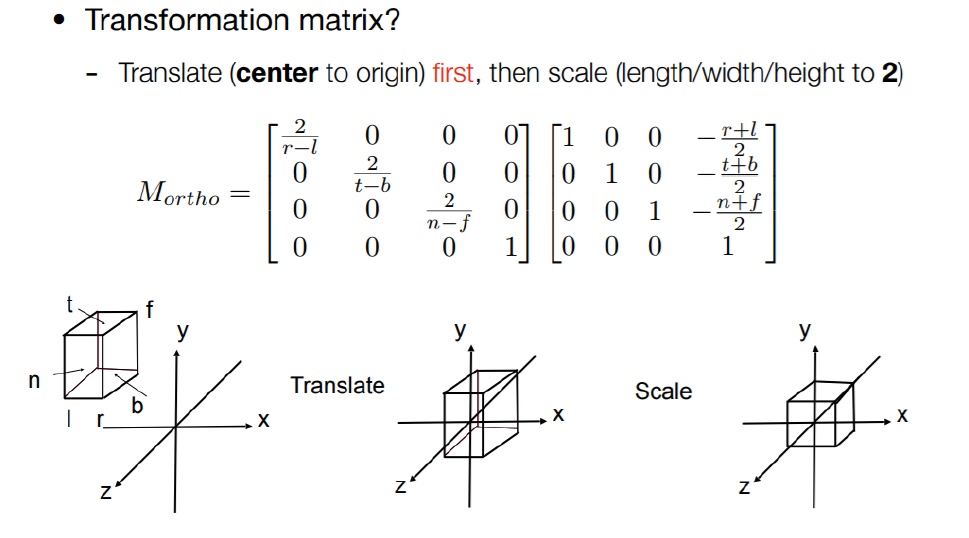
这个原始的立方体可以视作我们规定的可视范围,分别代表屏幕的长度,宽度,深度。我们通过变换矩阵将给定的立方体变换到[-1,1]^3的标准立方体上,只需先平移,再缩放。
透视投影: 把视锥体压缩成一个长方体,能够体现近大远小的视觉特点。
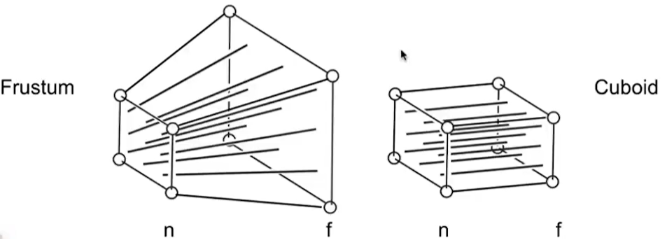
我们希望对视锥体中的每一个点,乘以一个变换矩阵,即可将其变换为长方体中的点。除此之外,我们还规定,变换前后,远平面和近平面上的点的z轴不变。
经过推导可以得到变换矩阵:[图形学笔记]推导投影矩阵 - 知乎 (zhihu.com)
通过这个矩阵,我们可以把原来的透视投影的视锥体压缩为正交投影的视锥体(长方体)。
最后我们再乘上一开始求出来正交投影矩阵Morth就得到了透视投影矩阵
此外,视锥体压缩成长方体以后,内部的点的z值更偏向于远平面