01 Review of Linear Algebra
01 Review of Linear Algebra
前置
图形学依赖于:
- 基础数学:线性代数,微积分,统计
- 基础物理学:光学,力学
- 其他:信号处理,数值分析
- 一点美学
向量
向量的概念
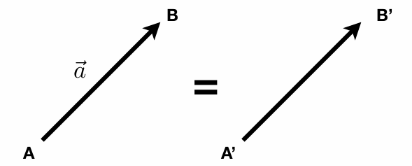
- 通常写作 $\vec{a}$ 或 $\mathbf{a}$
- 或者使用起点和终点来表示 $\vec{AB} = B - A$
- 有方向和长度
- 没有特定的起点
向量的归一化
- 向量的长度可以表示为 $|\vec{a}|$
单位向量
- 向量的模长为1
- 向量的归一化:$\hat{a} = \vec{a}/|\vec{a}|$
- 用来表示方向
向量加法
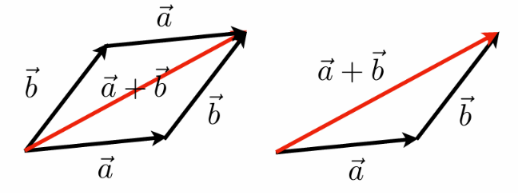
- 几何上:平行四边形定理和三角形定理
- 代数上:简单的坐标相加
笛卡尔坐标系
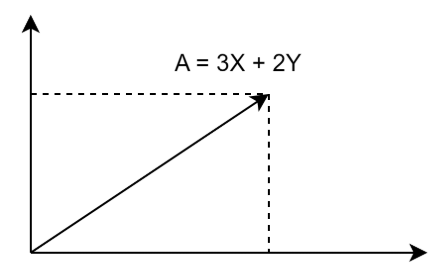
- X和Y是正交的单位向量
- 任一向量都可以用X和Y来表示
向量的点乘
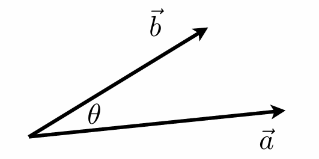
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta$
性质
- 交换律:$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$
- 分配律:$\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$
- 结合律:$(k\vec{a})\cdot\vec{b}=\vec{a}\cdot(k\vec{b})=k(\vec{a}\cdot\vec{b})$
笛卡尔坐标系下的点乘
逐分量相乘后求和
2D
$\vec{a} \cdot \vec{b} = \begin{pmatrix} x_a \\ y_a\\ \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b\\ \end{pmatrix} = x_ax_b + y_ay_b$
3D
$\vec{a} \cdot \vec{b} = \begin{pmatrix} x_a \\ y_a\\ z_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b\\ z_b \end{pmatrix} = x_ax_b + y_ay_b + z_az_b$
图形学中的点乘
求出两个向量间的角度
衡量两个向量靠近的情况
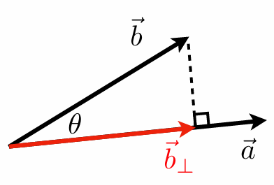
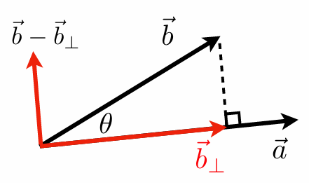
分解向量
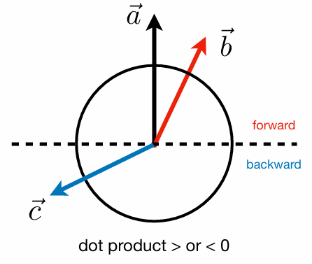
判断向前或向后的方向
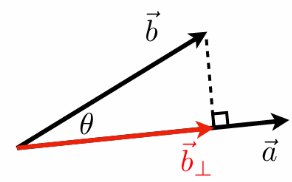
找到一个向量在另一个向量上的投影
向量的叉乘
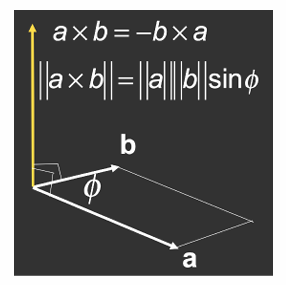
- 正交性:叉乘结果向量与两个初始向量都垂直。
- 方向确定:叉乘结果向量的方向由右手定则确定。
- 坐标系构建:叉乘在后续构建坐标系时非常有用。
叉乘公式
$a \times b = \begin{pmatrix} y_az_b - y_bz_a\\\\ z_ax_b - x_az_b\\\\ x_ay_b-y_ax_b \end{pmatrix}$
$\vec{a} \times \vec{b} = A * b = \begin{pmatrix} 0 & -z_a & y_a \\\ z_a & 0 &-x_a \\\ -y_a & x_a & 0 \\ \end{pmatrix} \begin{pmatrix} x_b\\\\ y_b\\\\ z_b\\\\ \end{pmatrix}$
图形学中的叉乘
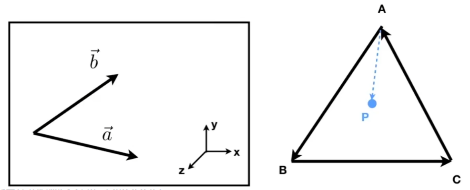
- 判定左和右
- 判定内与外
其他
在实际应用中,会存在多个坐标系统,例如:
- 全局坐标系统(Global)
- 局部坐标系统(Local)
- 世界坐标系统(World)
- 模型坐标系统(Model)
- 模型的部件坐标系统(如头部、手部等)
关键问题在于如何在这些不同的坐标系统之间进行转换(将在下周的课程探讨)
矩阵
矩阵乘法
A矩阵的列数必须 = B矩阵的行数(M×N)(N×P) = (M×P)
$\begin{pmatrix} 1&3\\ 5&2\\ 0&4 \end{pmatrix} \begin{pmatrix} 3&6&9&4\\ 2&7&8&3\\ \end{pmatrix} = \begin{pmatrix} 9&?&33&13\\ 19&44&61&26\\ 8&28&32&? \end{pmatrix}$
性质:
- 不满足交换律:AB 和 BA 结果不同
- 满足结合律和分配律
转置矩阵
$A = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} \qquad A^T = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ \end{pmatrix} $
- 交换矩阵的行和列
- $(AB)^T = B^TA^T$
逆矩阵
$I_{3\times3} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad AA^{-1} = A^{-1}A = I \qquad (AB)^{-1} = B^{-1}A^{-1}$
矩阵中的向量乘法
点乘
$\vec{a} \cdot \vec{b} = \vec{a}^T \vec{b} = \begin{pmatrix} x_a & y_a & z_a \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = (x_a x_b + y_a y_b + z_a z_b)$
叉乘
$\vec{a} \times \vec{b} = A^* b = \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix}$